Kaynaklar:
Introduction to the Design & Analysis of Algorithms 3e - Pearson
@elif_haytaoglu

Decrease and Conquer

Bu yaklaşımda; verilen problemlere çözüm bulmak amacıyla problemden daha küçük boyuttaki örneğine çözüm aranır. Daha küçük boyutu için bulunan çözüm ana probleme uygulanır.

Yaklaşımın üç çeşidi bulunur:

• Decrease by a constant (sabit bir sayı ile azaltma)
• Decrease by a constant factor (sabit bir çarpan ile azaltma)
• Variable size decrease (değişken boyutta azaltma)

Decrease-by-a-constant Algoritmaları

İşleyeceğimiz ilk çeşit olan decrease-by-a-constant yaklaşımında, değişken sayısı her aşamada belli bir sabit sayı kadar azaltılarak (bu sabit sayı genellikle 1 olarak seçilir), çözüm bulunmaya çalışılır.

1 azaltma olarak yapılan haline decrease-by-one da denir.

Insertion Sort

Decrease-by-one yaklaşımı ile liste sıralanmasına Insertion Sort iyi bir örnektir. Algoritmanın mantığı şu şekildedir; sıralanması gereken listenin daha ufak bir bölümü sıralı gibi kabul edilir ve seçilen pivot bu mantıkla sırada durması gerektiği yere yerleştirilir.

Örnek vermek gerekirse, elinizde bir deste kart var gibi düşünün. Sıralamak için baktığınız karttan geriye dönük olarak giderek gereken yere koyarsınız. Insertion Sort tam olarak bu kart sıralamasının yapılmasıdır.

Sözde kodu:

def insertion_sort(list)
  for i : 1 to n-1 do
    v = list[i]
    j = i-1
    while j >= 0 AND list[j] > v do
      list[j+1] = list[j]
      j--
    list[j+1] = v

Algoritmadaki ana işlem list[j] > v kontrolüdür.

Büyüme hızı;
En kötü: Θ(n^2)
En iyi: Θ(n)
Ortalama: Θ(n^2)

Topological Sorting

Topological Sorting, yalnızca yönlü ağaçlarda uygulanabilen bir sıralama algoritmasıdır. Agaçtan kendisine bir girdi olmayan parçaların koparılma sırası olarak düşünülebilir. Paket yöneticileri, görev talimatları gibi uygulamalarda kullanılır.

Topological Sorting uygulayabileceğimiz yollardan bir tanesi; tüm vertex’lerin taranması ve herhangi bir girdisi olmayan vertex’lerin çıkarılmasıdır.

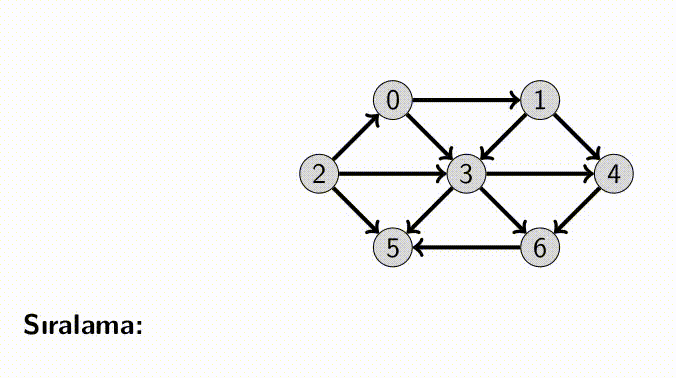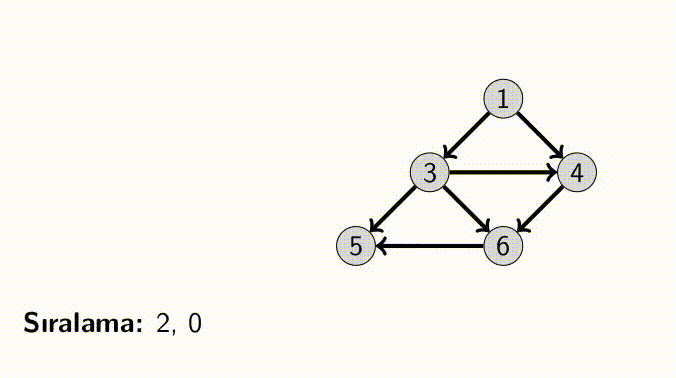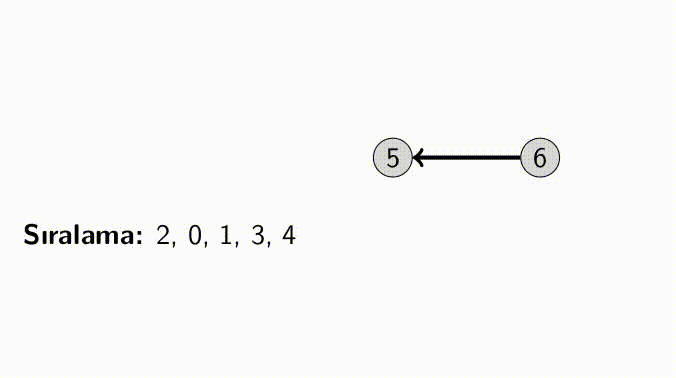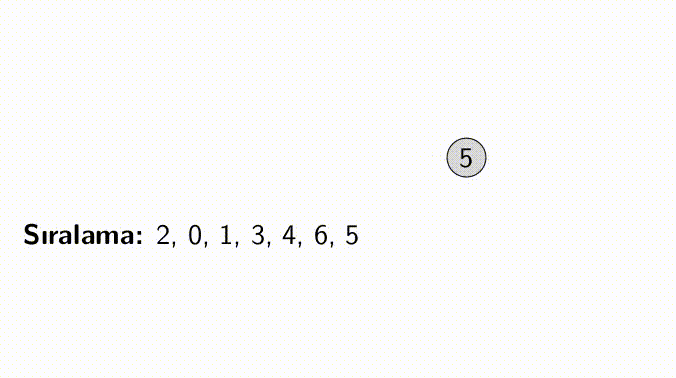
Diğer bir yol ise; ilgili ağaçta DFS olarak dolaşmak ve bu dolaşma sırasının tersini almaktır. Tersi alanmış bu sıra bize Topological Sorting sıralamasını verecektir.

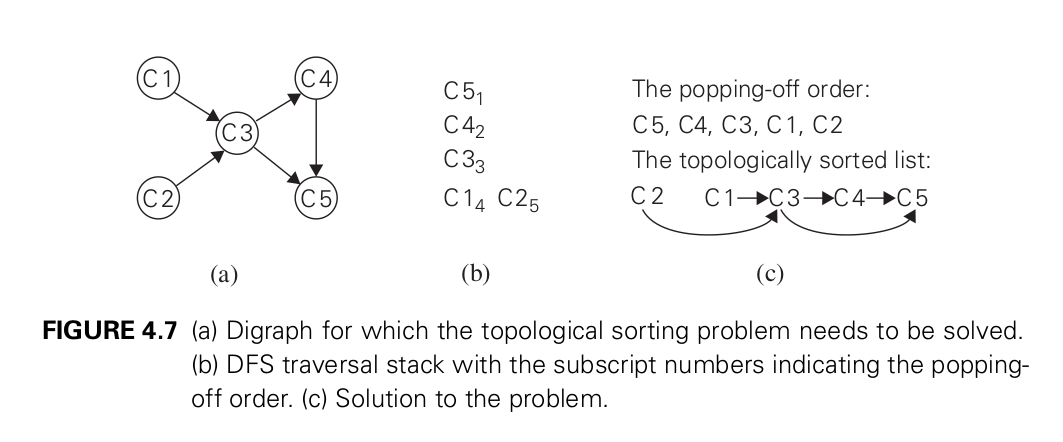
Döngü içeren ağaçlara (yani DFS dolaşımında backforward içeren ağaçlara) Topological Sorting uygulanamaz. Örneğin aşağıdaki gibi bir ağaca Topological Sorting uygulanamaz.

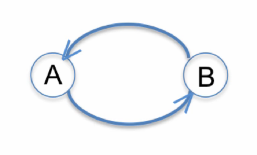
Kombinasyon Nesneleri Oluşturmak için Algoritmalar

Bu bölümde kombinasyon nesneleri olan; alt kümeler ve permütasyonların oluşturulmaları için kullanılan algoritmaları inceleyeceğiz.

Permütasyon Oluşturmak

1’den n’ye kadar olan sayıların permütasyonları istense nasıl bulursunuz ?
John Trotter algoritması ile bunu oldukça pratik bir yoldan bulabiliriz.

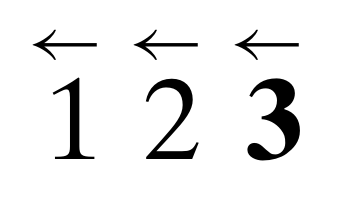
• İlk olarak tüm sayılara yukardaki gibi bir yön verilir
• En büyük eleman mobil olarak seçilir (kalın olarak yazılan)
• Mobil eleman ok yönüne doğru hareket ettirilir
• Mobil değiştitiğinde kendisinden daha büyük bir sayı var mı diye bakılır
• Eğer var ise, büyük olan sayının yönü değiştirilerek mobil yapılır
• Hiç bir mobil kalmayasaya kadar bu şekilde devam eder

Sözde kodu:

def john_trotter(list):
  initialize the list with arrow as the first permutation
  while the last permutaion has a mobile element do
    find its largest mobile element k
    swap k with the adjacent k s arrow points to
    reverse the direction of all the elements that are larger than k
    add the new permutaion to the list

Büyüme hızı: Ө(n!)

Alt Küme Oluşturma

Bir kümenin tüm alt kümelerini bulmak gerekiyor olsun. Bunun için oldukça basit bir mantık vardır; ikilik tabandan yararlanmak.

3 elemanlı bir küme olsun, o halde ikilik tabanda 111’e kadar yazarsak tüm alt kümeleri bulmuş oluruz.

Yani aşağıdaki gibi tüm alt kümeleri bulabiliriz.

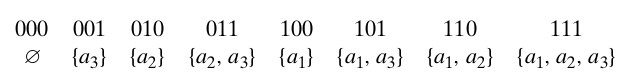
Decrease-by-a-constant-factor Algoritmaları

İkinci olarak işleyeceğimiz çeşit; decrease-by-a-constant-factor, yani sabit bir kat sayı ile azaltma. Bu yaklaşımda problem, verinin belli bir katta daha ufak hali ele alınarak çözülür.

Binary Search

İkili arama işlemi sıralı dizilerde aranan verinin bulunmasını sağlar.
Yaklaşım basittir. İlk olarak ortanca değere bakılır; ortanca değer ile aranan değer karşılaştıralarak sola ya da sağa gidilir. Bu algoritma recursive şekilde aranan veri bulunasaya ya da gidilecek yer kalmayasa kadar devam eder.

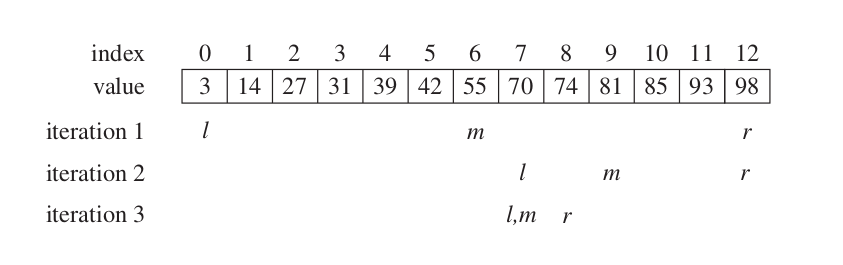
Sözde kodu:

def binary_search(list, key)
  if list[list.length/2] == key
    return list.length/2
  else if key > list[list.length/2]
    return binary_search(list.right_half, key)
  else
    return binary_search(list.left_half, key)

Algoritmanın mantığı recursive olarak kurulmuş olsa da non-recursive olarak yazmak ta mümkündür.

def binary_search_nonrecursive(list, key)
  left = 0
  right = list.length

  while counter <= left do
    median = ( counter + left ) / 2
    if key = list[median]
      return median
    else if key < list[median]
      right = median - 1
    else
      left = median + 1
  return -1

Algoritmanın çalışma mantığına göre,

T(n) = T(n/2) + 1, T(1) = 1

Buradan da,
Büyüme hızı: Θ(log2(n))

Fake-Coin Problem (sahte para problemi)

Elinizde bir avuç aynı cins bozuk para olduğunu hayal edin. Bu paralardan yalnızca biri sahte ve bu sahte olan para gerçek paraya göre daha hafif.
Sahte parayı nasıl bulursunuz ?

Decrease-by-a-constant yaklaşımı ile parayı logn’lik bir zamanda kolayca tespit edilebilir.

Elimizdeki para sayısı eğer tek ise, bir tanesini kenara ayırır ve kalan parayı (n-1)/2 olarak iki parçaya ayırarak tartarız. Eğer sonuç eşit ise ayırdığımız para sahtedir; eğer bir taraf daha hafif ise sahte para o gruptaki paralar arasındadır, o paraları da iki eş gruba ayırarak tartarız. Bu şekilde bölerek sahte parayı tespit edebiliriz.

Algoritmanın çalışma mantığına göre çalışma zaman büyüme hızı (binary search ile aynı mantıkta),

T(n) = T(n/2) + 1, T(1) = 0

Bu da Θ(log2(n))‘dir. Fakat bu algoritma geliştirilebilir. Eğer elimizdeki parayı 2’ye değil de 3’e bölerek işleme devam edersek çalışma zaman büyüme hızı azalacaktır.

T(n) = T(n/3) + 1, T(1) = 0

Bu da Θ(log3(n))‘dir.

Peki; Θ(log3(n)), Θ(log2(n))‘den kaç kat daha hızlıdır ?
log2(n) / log3(n) = 1,6 kat

Russian Peasant Multiplication (rus köylü çarpımı)

Ruslar tarafından geliştirilen, iki pozitif sayıyı daha kolay olarak çarpabilmeyi sağlayan bu algoritma aşağıdaki gibidir.

n ve m isimli iki tane pozitif sayı olsun elimizde.

Eğer n çift bir sayı ise, n . m = n/2 . 2m
Eğer n tek bir sayi ise, n . m = (n-1)/2 . 2m + m

Olarak işlemi güncelleriz. İşlem 1 . m = m olasaya kadar devam eder ve elimizde son kalan değer çarpma işleminin sonucu olmuş olur.

50 ve 65 sayılarını çarpmak istiyor olalım, işlem aşağıdaki gibi olacaktır.

Josephus Problem

Flavius Josephus, Roma’lılara karşı bir isyanı yönetmiş tarihi bir karakterdir. Roma’lılar tarafından etrafları sarıldığında ve isyankarlar teslim olmak yerine ölmeyi tercih ettiklerinde, kişilerin intihar etmeden ölebilmeleri için herkesin birbirini öldüreceği, son ayakta kalan kişinin de kendisini öldürmesi gerektiği bir sistem ortaya atmıştır. Bu şekilde neredeyse tüm isyanlarlar (kendini öldürecek olan bir kişi hariç) intihar etmeden canlarına son verebilecekti.

Fakat Josephus bu fikri ortaya atarken aklında ölmek gibi bir fikir yoktu. En son hayatta kalacak kişinin yerin durmalı ve ardından kendini öldürmek yerine Roma’lılara teslim olmalıydı. Peki tam olarak nerede durmalıydı ?

Aşağıdaki gibi adamların bir çember yapıp, saat yönünde ilerleyerek birbirini öldürdüğü düşünün. Yani 1 2’yi, 3 4’ü, 5 6’yı, 1 3’ü, 5 1’i öldürecektir.

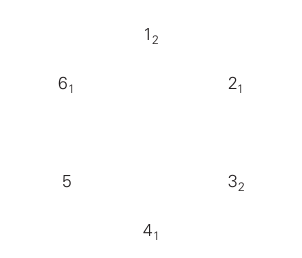
6 kişilik bu örnekte en son ayakta kalan adam 5 numaralı yerde duran olacaktır.

En son hayatta kalan kişinin konumunu bulmanın basit bir yolu vardır. Kişi sayısı ikilik tabanda yazılır, ardından sola doğru bir kayma işlemi yapılır (en soldaki rakamın en sağa atılması), çıkan ikilik tabandaki sayının onluk tabandaki karşılığı Josephus’un durması gerektiği noktayı gösterecektir.

J(5) = J(1 0 1) = 0 1 1 = 3,
J(6) = J(1 1 0) = 1 0 1 = 5,
J(7) = J(1 1 1) = 1 1 1 = 7,
J(8) = J(1 0 0 0) = 0 0 0 1 = 1